Ocean turbulence statistics interpreted as the signature of IG waves¶
temporal spectra: $\omega^{-2}$ between $f$ and $N$
vertical spectra: $N^2 k_z^{-3}$
horizontal spectra: $k_h^{-5/3}$ at quite large scales

"Garrett-Munk spectrum", interpretations?¶
Naive representation: soup - cascade of (weakly interacting) IG waves?
More advanced theories based on IG waves (weak wave turbulence, ...)
Problems:¶
Validity of the weak wave turbulence solutions?
Not obtained in the lab: neither experimentally nor numerically
Toroidal/poloidal decomposition of an incompressible flow¶
Kinematic decomposition:
- $\omega_z$ (toroidal = "vortical")
- $\boldsymbol\nabla_h \boldsymbol{v}_h$ and $v_z$ (poloidal)
- shear modes
Case stratification without system rotation $f = 0$¶
Equation for $\omega_z$:
$$ D_t \omega_z = \boldsymbol\omega \cdot \boldsymbol\nabla \boldsymbol{v} + \nu \boldsymbol\nabla^2 \omega_z$$$\Rightarrow$ No inviscid linear term
Linear limit: poloidal velocity = internal waves
Strongly stratified turbulence¶
For oceanic parameters (strongly stratified $F_h\ll 1$, weakly dissipative $\mathcal{R} = Re {F_h}^2 > 10$):
LAST regime: "Layered Anisotropic Stratified Turbulence"
Strongly non-linear
$\omega_z \sim \nabla_h u$

- Possible interpretation of oceanic data (Riley & Lindborg, 2008)
IG wave turbulence in the Coriolis platform¶
Savaro et al. (2020): Generation of weakly nonlinear turbulence of internal gravity waves in the coriolis facility

$+$ other experiments (presented today by Costaza Roda)
Reproduction / extensions of these experiments with idealized simulations¶
Pseudo-spectral Fourier, periodic over $x$, $y$ and $z$
Navier-Stokes under the Boussinesq approx. Constant $N$
Immersed boundary method to mimic the experimental forcing

$ L = 12\,$m and $H = 2\,$m to force the same modes as in the exp.
Suppress some modes (shear modes and waves at $k_z = 0 \Leftrightarrow \omega=N$)
Experimental parameters ($N$, $\nu$)
quasi-DNS (newtonian $\nu$ + a bit of hyperviscosity $\nu_4$)
Up to $2304\times2304\times384$ grid points
Few results for a set of parameters used in the experimental paper¶
$F = \frac{\omega_f}{N} = 0.73$ and $a = 0.5\,$cm.

We obtain statistically stationary flows¶

Dissipation only at small scales $\Rightarrow$ energy transfers towards "small scales" (warning: anisotropy)
Snapshot: vertical cross-section $b$¶

Small vertical length scales
Warning: dissipation at large horizontal scales even for large $Re$
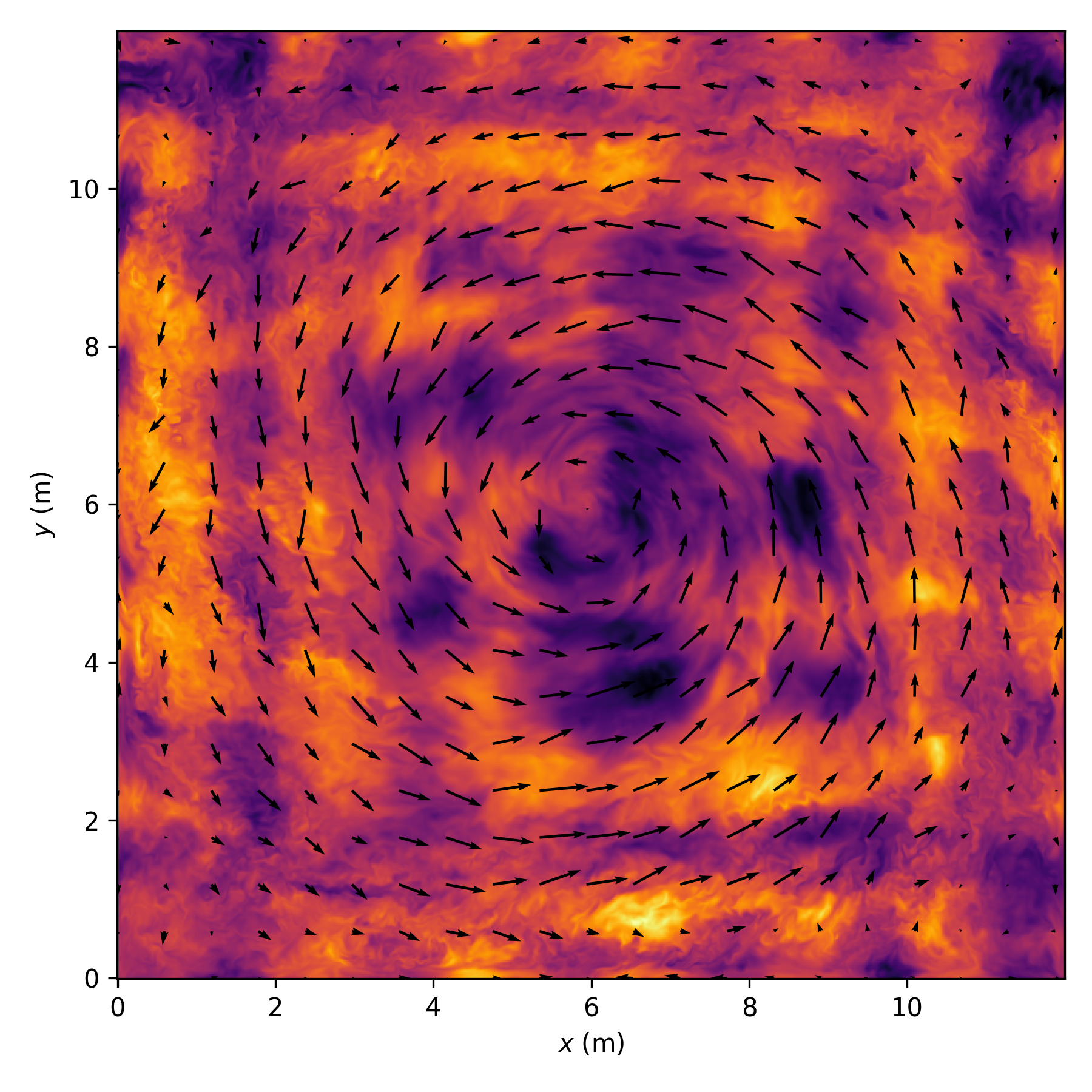
Snapshot: horizontal cross-section $b$ and $\boldsymbol{v}$¶
Big vertically superposed horizontal vortices.
Horizontal and vertical spectra¶

Frequency spectra¶

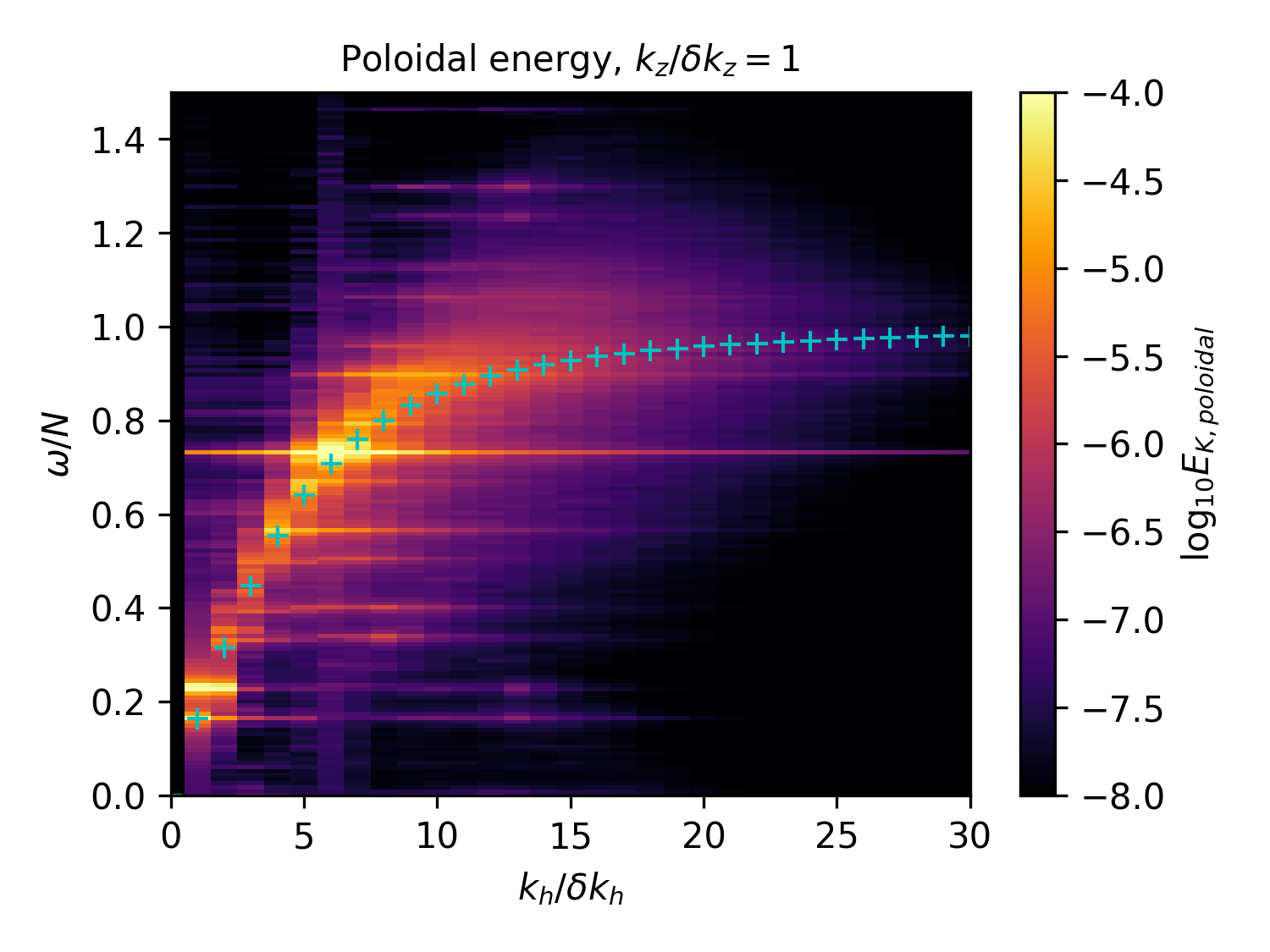
Spatio-temporal spectra¶

Spatio-temporal spectra¶
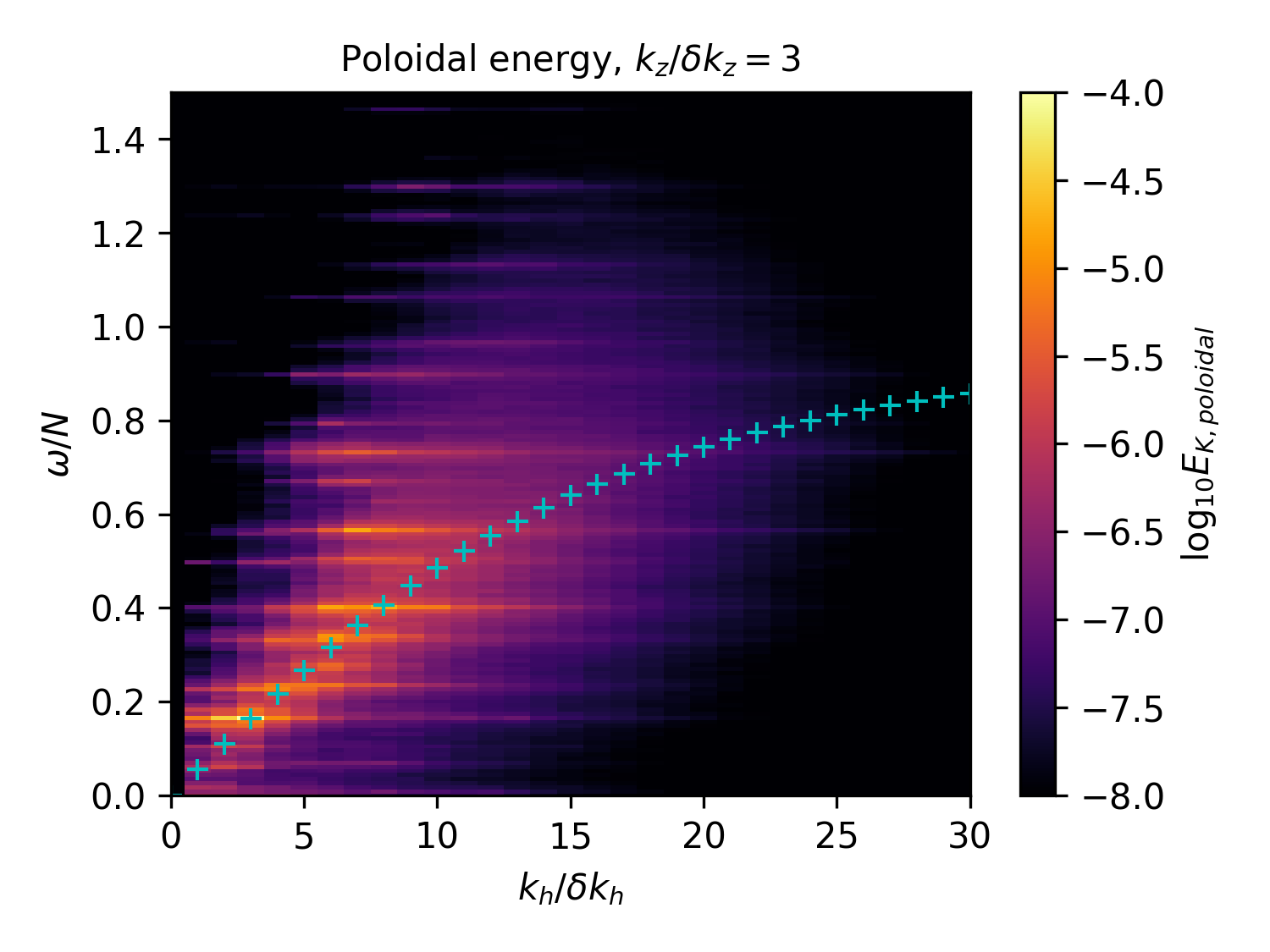
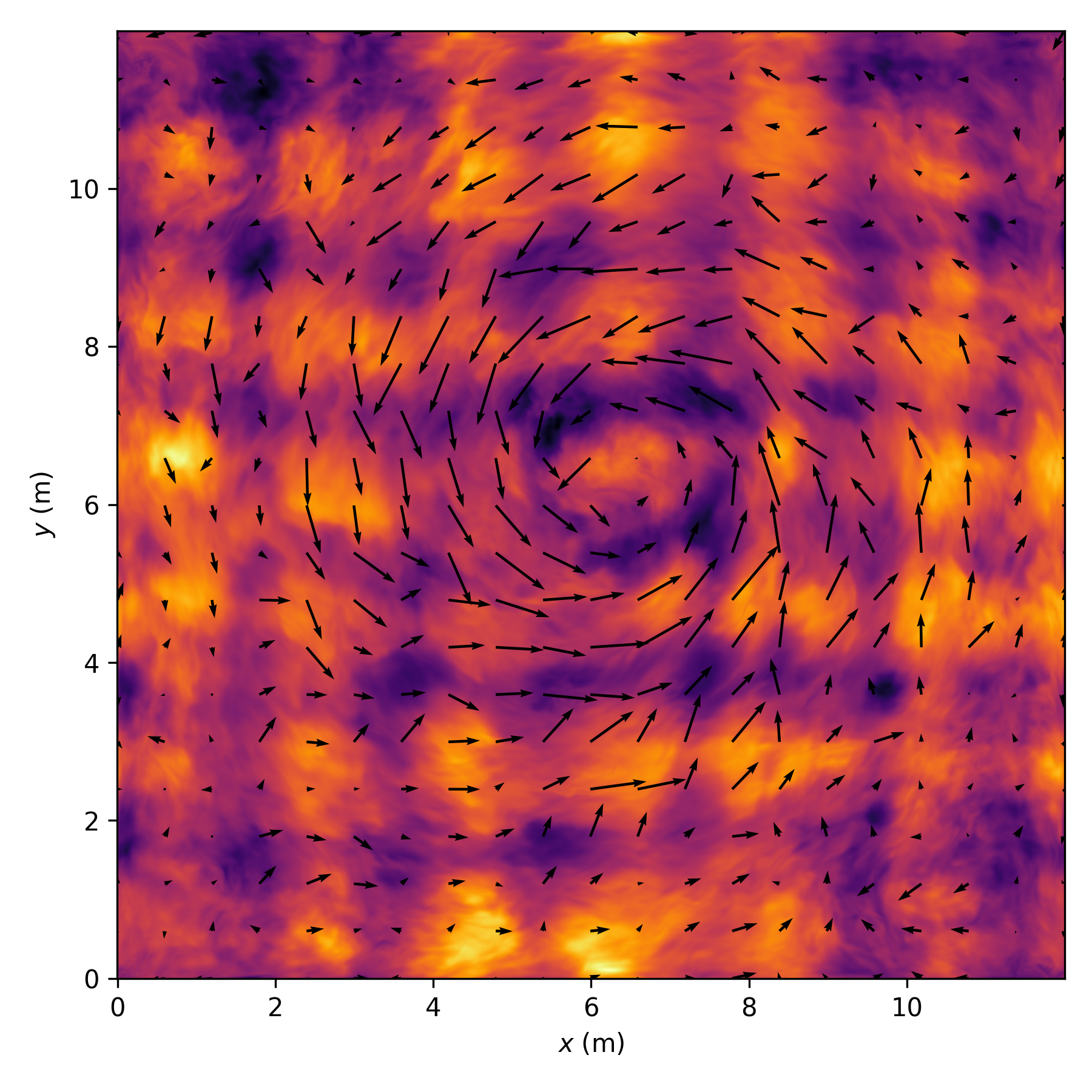
Let's force slower... $F = \omega_f / N = 0.4$¶


The code is interesting: FluidSim¶

Open-source collaborative framework / library for writting solvers
Quality code (continuous integration, proper documentation, issue tracker)
Very user-friendly
Developer friendly: mostly in Python, highly modular (object-oriented Python)
Extensible (for example snek5000)
Specialized in pseudo-spectral (Fourier), but not only
Very efficient
The code is interesting: FluidSim¶

To try it and reproduce these results:¶
conda create -n env_fluidsim fluidsim "fluidfft[build=mpi*]" "h5py[build=mpi*]" ipython
conda activate env_fluidsim
...
Conclusions¶
Experiments extented with idealized numerical simulations
Gravity waves + large vortices ("condensate")
Weakly nonlinear waves only for small $k_z/\delta k_z$
Quite small buoyancy Reynolds number even in the Coriolis platform
Limitations inherent to the experimental setup (small $a$, small $N$)
Experimental forcing non local in $\boldsymbol{k}$-space + very intermittent
Need to force at small $\frac{\omega_f}{N}$ (i.e. $k_{fz} > k_{fh}$) to get $\omega^{-2}$