Numerical study of experimentally inspired stratified turbulence forced by waves¶

Jason Reneuve, Pierre Augier and Nicolas Mordant
Université Grenoble Alpes, CNRS, Grenoble INP, LEGI, Grenoble
           
4th July 2022
$$\require{begingroup}\require{newcommand}$$$$\gdef\vec#1{\boldsymbol{#1}}$$$$\gdef\R{\mathcal{R}}$$$$\gdef\FhR{(F_h,\ \R)}$$

Internal gravity wave turbulence in the lab?¶

Oceanic and atmospheric measurements interpreted as IGW turbulence

Reproducible in the lab?

Stable density stratification $\Rightarrow$ Waves (IGW) and "vortices" ($\omega_z$)

Stratified turbulence (forced by vortices)

  • Horizontal Froude number $F_h$ and buoyancy Reynolds number $\R = Re {F_h}^2$

  • LAST regime $F_h<0.02$, $\R>20$: downscale energy cascade and anisotropic spectra

$$b(x,z)$$
Brethouwer, Billant, Chomaz & Lindborg (2007)

  • $\R = Re {F_h}^2 > 20 \Rightarrow Re \gg 1$

    • experiments: very large apparatus
    • simulations: high resolution

Internal gravity wave turbulence in the Coriolis facility!¶

Coriolis platform in Grenoble

  • 13m-diameter, 1m-deep, 130 tons water
  • stratification with salt
  • rotation up to 6 rpm
Sorry, your browser doesn't support embedded videos.

Internal gravity wave turbulence in the Coriolis facility!¶

Linearly stratified ($\sim$ 1 ton of salt)

Savaro et al. PRFluids 2020

Internal gravity wave turbulence in the Coriolis facility!¶

Sorry, your browser doesn't support embedded videos.
Sorry, your browser doesn't support embedded videos.

Internal gravity wave turbulence in the Coriolis facility¶

Temporal spectra for different forcing amplitudes¶

Savaro et al. PRFluids 2020

Numerical setup: experimentally inspired stratified turbulence forced by waves¶

  • Pseudo spectral solver ns3d.strat of the open-source CFD framework Fluidsim

  • 3D periodic!

Basically same parameters than for the experiments in the Coriolis platform: size, viscosity, Brunt-Väisälä frequency $N=0.6$ rad/s, forcing frequency $\omega_f = 0.73 N$ and forcing amplitude.

$\Rightarrow$ high resolution (up to $2304\times2304\times384$) and very long time (typically 15 h)

Numerical setup: experimentally inspired stratified turbulence forced by waves¶

$2\pi / N \simeq 10$ s, $2\pi / \omega_f \simeq 15$ s

  • Long simulations at different resolution ($240\times240\times40$, $480\times480\times80$, $1152\times1152\times192$ and $2304\times2304\times384$)

  • Hyper viscosity is decreased when resolution is increased

  • $2304\times2304\times384$ quasi DNS

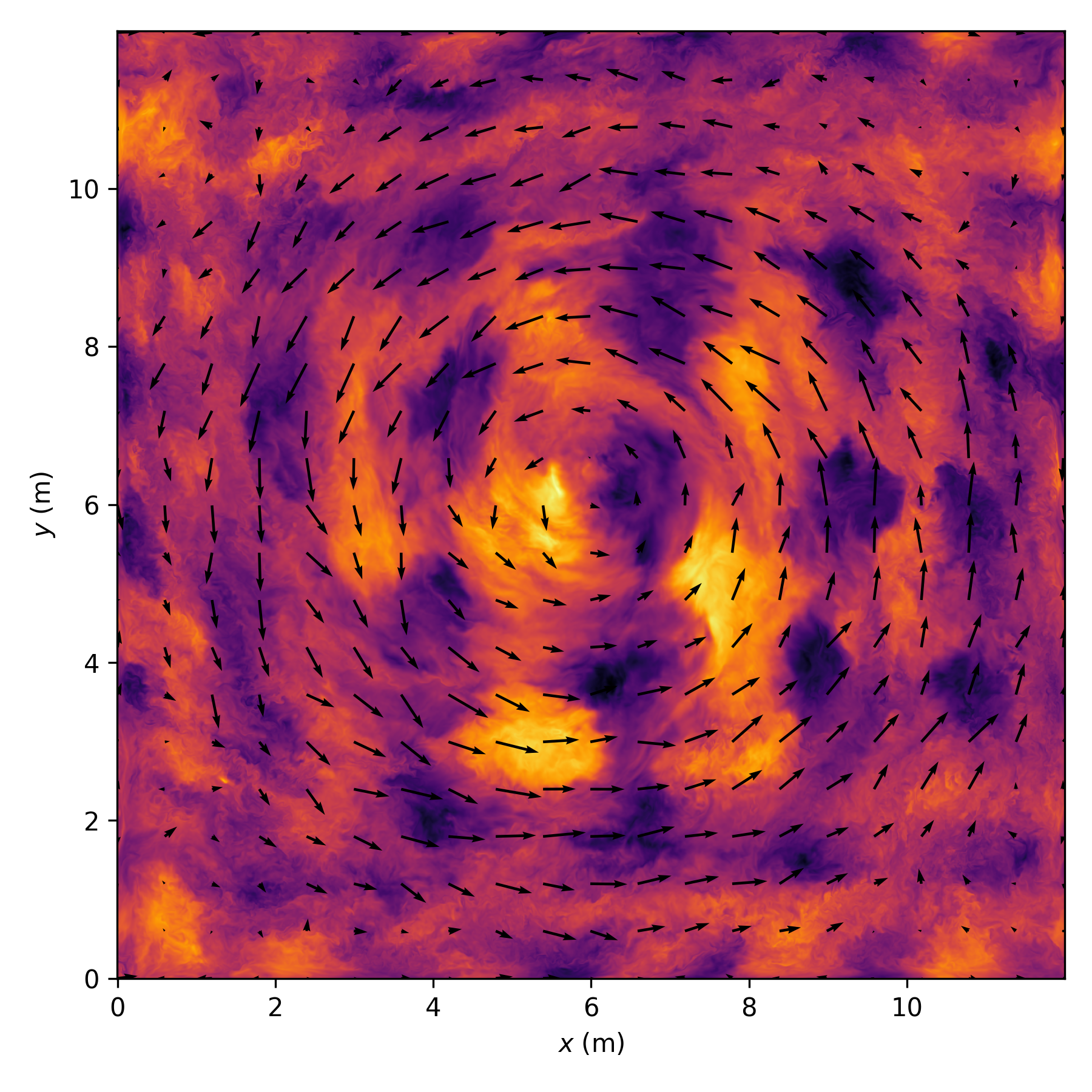
  • Strong vortical flow!

  • Stationarity?


Response to the forcing: $U_h$ and $\varepsilon_K$

$\Rightarrow F_h \simeq 6.5 \times 10^{{-4}}$ (strongly stratified) and $\R = Re {F_h}^2 \simeq 0.5$ (viscosity affected regime)

Snapshots for $\omega_f = 0.73N$ and $a = 5$ cm¶

  • large scale waves

  • small scale "turbulence"

  • thin vertical layers

  • 2 counter-rotating vortices

Mean flow: comparison simulation / experiment¶

Horizontal cross-section¶

2 counter-rotating vortices at 2 $\neq$ levels

Temporal spectra for $\omega_f = 0.73 N$ and $a = 5$ cm¶

Triads involving the forced frequency and modes of the numerical domain

Vortical flow dominates at very small frequency

Continuum between the peaks

Spatial spectra for $\omega_f = 0.73 N$ and $a = 5$ cm¶

Very strongly anisotropic spectra ("strongly stratified", $F_h \ll 10^{-2}$)

Viscosity affected flow ($\R \simeq 0.5$) but not far from the transition $\R > 1$

Spatio-temporal spectra for $\omega_f = 0.73 N$ and $a = 5$ cm¶

Triad: $\omega_1 + \omega_2 = \omega_f$ and $\vec{k}_1 + \vec{k}_2 = \vec{k}_f$

Spatio-temporal spectra for $\omega_f = 0.73 N$ and $a = 5$ cm¶

Weakly non linear waves only for first vertical modes

Stronger forcing for $\omega_f = 0.73 N$: $a=10$ cm¶

$a = 0.05$ cm ($\R \simeq 0.5$)
$a = 0.10$ cm ($\R \simeq 6.5$)

Stronger forcing for $\omega_f = 0.73 N$: $a=10$ cm¶

Temporal spectra¶

$a = 0.05$ cm ($\R \simeq 0.5$)
$a = 0.10$ cm ($\R \simeq 6.5$)

Stronger forcing for $\omega_f = 0.73 N$: $a=10$ cm¶

Spatial spectra¶

$a = 0.05$ cm ($\R \simeq 0.5$)
$a = 0.10$ cm ($\R \simeq 6.5$)

Slower forcing $\omega_f = 0.4 N$ and $a=10$ cm¶

Temporal spectra¶

$\omega_f = 0.73 N$
$\omega_f = 0.40 N$

Conclusions¶

  • Pseudo spectral 3D periodic simulations with penalization can reproduce some aspects of the dynamics observed in experiments

  • The buoyancy Reynolds number $\R$ is crucial (transition at $\R \gtrsim 1$)

  • Accumulation of energy at large scales (2 counter-rotating vortices and waves)

  • Tank and forcing geometry $\Rightarrow$ normal modes ($\neq$ solutions for exp. and simulations...)

  • "Wave turbulence" between the modes

  • Not far from $\omega^{-2}$ between $\omega_f$ and $N$

Note: Fluidsim (https://fluidsim.readthedocs.io) is now a great tool!¶

conda create -n env-fluidsim ipython fluidsim "fluidfft[build=mpi*]" "h5py[build=mpi*]"