Hydraulique à surface libre
L'un des objectifs majeurs de mon travail de recherche est de dériver un modèle moyenné sur la profondeur capable de décrire les écoulements rapidement variés tels que les ressauts hydrauliques ou les trains de rouleaux (roll waves). Ces écoulements sont caractérisés par une zone de recirculation très turbulente, souvent décrite comme un rouleau (roller).
Dans le film ci-dessous, pris dans un ressaut hydraulique naturel du Verdon, une petite balle est lâchée en amont (ici à gauche) du ressaut. L'écoulement transporte rapidement la balle vers l'aval dans le ressaut où son mouvement devient très erratique. La balle est prise dans la zone de recirculation turbulente, apparaît par moments à la surface libre. Elle est ramenée vers l'amont jusqu'au début du ressaut avant de disparaître à nouveau et d'être entraînée vers l'aval du ressaut.
Les trois prises de vue suivantes, présentées dans l'ordre chronologique, montrent l'effet de recirculation dans le ressaut : 1) La balle arrive de l'amont dans le ressaut; 2) Elle est prise dans le rouleau et remonte à la surface libre; 3) Elle revient vers l'amont jusqu'au début du ressaut.



Dans les équations de Saint-Venant, qui constituent les équations de base en hydraulique à surface libre, ces écoulements rapidement variés sont décrits comme des discontinuités, c'est-à-dire des variations brutales de profondeur et de vitesse. La structure de l'écoulement (profil de profondeur par exemple) n'est pas décrit. Ceci est dû au fait que les équations de Saint-Venant supposent une vitesse à peu près uniforme dans la profondeur alors que, dans ce type d'écoulement, le cisaillement et la turbulence sont très importants.
Dans le modèle hyperbolique dérivé dans ma thèse de doctorat (Richard & Gavrilyuk 2013), la turbulence et le cisaillement sont explicitement pris en compte par une variable supplémentaire, homogène au carré d'une vorticité, appelée enstrophie. Celle-ci se décompose en deux termes : une enstrophie décrivant le cisaillement et la turbulence sur le fond et une entrophie pour le cisaillement et la turbulence du rouleau turbulent. L'équation de l'énergie devient une équation indépendante fondamentale du modèle. Un ressaut ou le front d'un rouleau comprend deux parties : 1) une petite discontinuité de profondeur mais qui correspond à une forte création d'enstrophie ; 2) une augmentation continue de profondeur, correspondant à une dissipation de l'enstrophie créée. La modélisation de la dissipation est cruciale dans ce type d'approche. La création d'enstrophie et sa dissipation peuvent aussi être décrites en termes de création et de dissipation d'énergie turbulente.
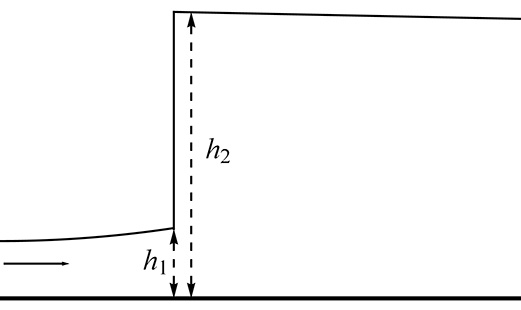
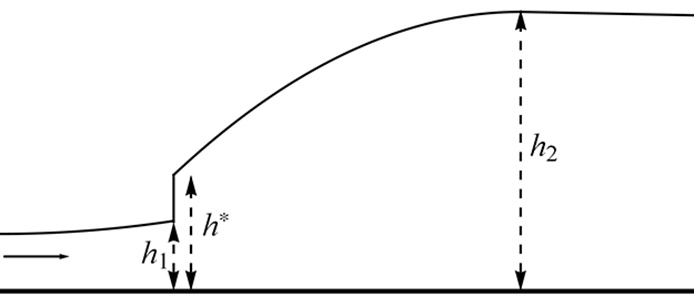
Le schéma de gauche présente un ressaut hydraulique tel qu'il est décrit par le modèle de Saint-Venant : une discontinuité. Le rapport de la profondeur aval sur la profondeur amont est donné par la relation de Bélanger, qui découle des relations de saut. Le schéma de droite présente un ressaut hydraulique décrit par le modèle de Richard & Gavrilyuk (2013) : un petit saut de profondeur (mais une forte création d'enstrophie) suivi d'un profil continu où la profondeur augmente (et où l'enstrophie décroît). La prise en compte du cisaillement sur le fond entraîne des écarts à la relation de Bélanger.
La résolution numérique montre que le modèle est capable de capturer les oscillations du ressaut hydraulique, aussi bien les oscillations de sa position que de sa surface libre.
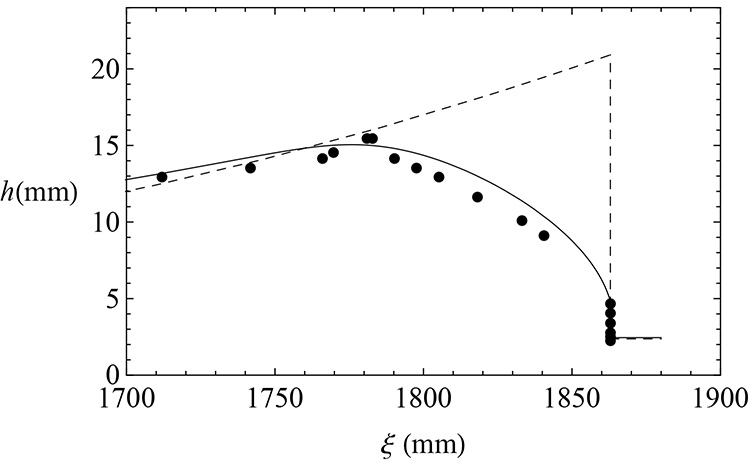
Les améliorations apportées par cette approche sont similaires pour les trains de rouleaux. La figure ci-dessous présente des mesures expérimentales (Brock 1967) de la profondeur dans la région du front de la vague (points noirs), la solution de Dressler (1949) basée sur les équations de Saint-Venant (pointillés) et la solution obtenue avec le nouveau modèle (trait plein, Richard 2013). La solution de Dressler décrit le front de la vague comme une discontinuité, ce qui correspond à une "épaisseur de choc" nulle. Le nouveau modèle permet de décrire cette épaisseur, en accord avec les expériences. La solution se compose d'une petite discontinuité de profondeur avec forte création d'énergie turbulente (front de vague "blanc" du fait de la présence d'écume) suivie d'une augmentation progressive de profondeur (dissipation de l'énergie turbulente) jusqu'à un maximum de profondeur.
Les photos ci-dessous montrent des trains de rouleaux dans le déversoir de la micro-centrale hydro-électrique de la Schappe à Briançon (Hautes-Alpes) et d'autres, beaucoup plus forts, dans le déversoir du barrage de Llyn Brianne (Pays de Galles).



La turbulence, le cisaillement et le frottement dus à l'interaction entre l'écoulement et le fond peuvent être modélisés par une méthode asymptotique. Ce travail a été réalisé dans Richard, Rambaud & Vila (2017) dans le cas d'un fond lisse. Un premier adimensionnement de type eau peu profonde (ou onde longue) conduit à des expressions pour les développements asymptotiques des variables de l'écoulement (vitesse, pression, tenseur des contraintes). Le modèle de turbulence utilisé est de type longueur de mélange. Le champ de vitesse obtenu diverge au voisinage de la paroi (loi log). Un deuxième adimensionnement de type visqueux doit être utilisé pour décrire l'écoulement au voisinage de la paroi. On obtient ainsi une deuxième série d'expressions pour les développements asymptotiques des variables de l'écoulement. Une procédure de raccordement asymptotique est alors mise en oeuvre pour raccorder les deux développements dans une zone de raccord. Cette procédure permet d'obtenir les expressions complètes des développements asymptotiques et des grandeurs moyennées sur la profondeur.
On peut alors dériver un modèle consistant moyenné sur la profondeur. À l'ordre le plus bas, les équations de Saint-Venant sont obtenues avec les expressions classiques du coefficient de frottement. À un ordre plus élevé, on obtient des corrections dues au cisaillement (le profil de vitesse n'est pas uniforme sur la verticale) et des termes correctifs sur le frottement et sur la dissipation d'énergie. Le modèle comporte alors trois équations (masse, quantité de mouvement, énergie) et trois variables (profondeur, vitesse moyenne, enstrophie).
Ces termes correctifs permettent de revisiter la question de la pente de frottement et de la pente d'énergie ainsi que les courbes de remous. On obtient aussi une bonne modélisation du cisaillement pour les écoulements rapidement variés.








