Abstract ¶

Stratified flows forced by internal waves similar to those obtained in the Coriolis platform (LEGI, Grenoble, France) [1] are studied by pseudospectral triply-periodic simulations. The experimental forcing mechanism consisting in large oscillating vertical panels is mimicked by a penalization method. The analysis of temporal and spatiotemporal spectra reveals that the flow for the strongest forcing in the experiments is composed of two superposed large and quasi-steady horizontal vortices, of internal waves in box modes and of much weaker waves outside the modes. Spatial spectra and spectral energy budget confirm that the flow is in an intermediate regime for very small horizontal Froude number \(F_h\) and buoyancy Reynolds number \(\mathcal{R}\) close to unity. Since the forcing frequency \(\omega_f\) is just slightly smaller than the Brunt-Väisälä frequency \(N\) , there are energy transfers towards slower waves and large vortices, which correspond to an upscale energy flux over the horizontal.

Two other experimentally feasible sets of parameters are investigated. A larger amplitude forcing shows that it would indeed be possible to produce in huge apparatus like the Coriolis platform stratified turbulence forced by waves for small \(F_h\) and buoyancy Reynolds number \(\mathcal{R}\) of order 10. Forcing slower waves for \(\omega_f = 0.40 N\) leaves space between \(\omega_f\) and \(N\) for “down-time-scale” transfers through weakly nonlinear interactions with temporal spectra consistent with \(\omega^{-2}\) slope. However, for this set of parameters, the large scales of the flow are strongly dissipative and there is no downscale energy cascade.

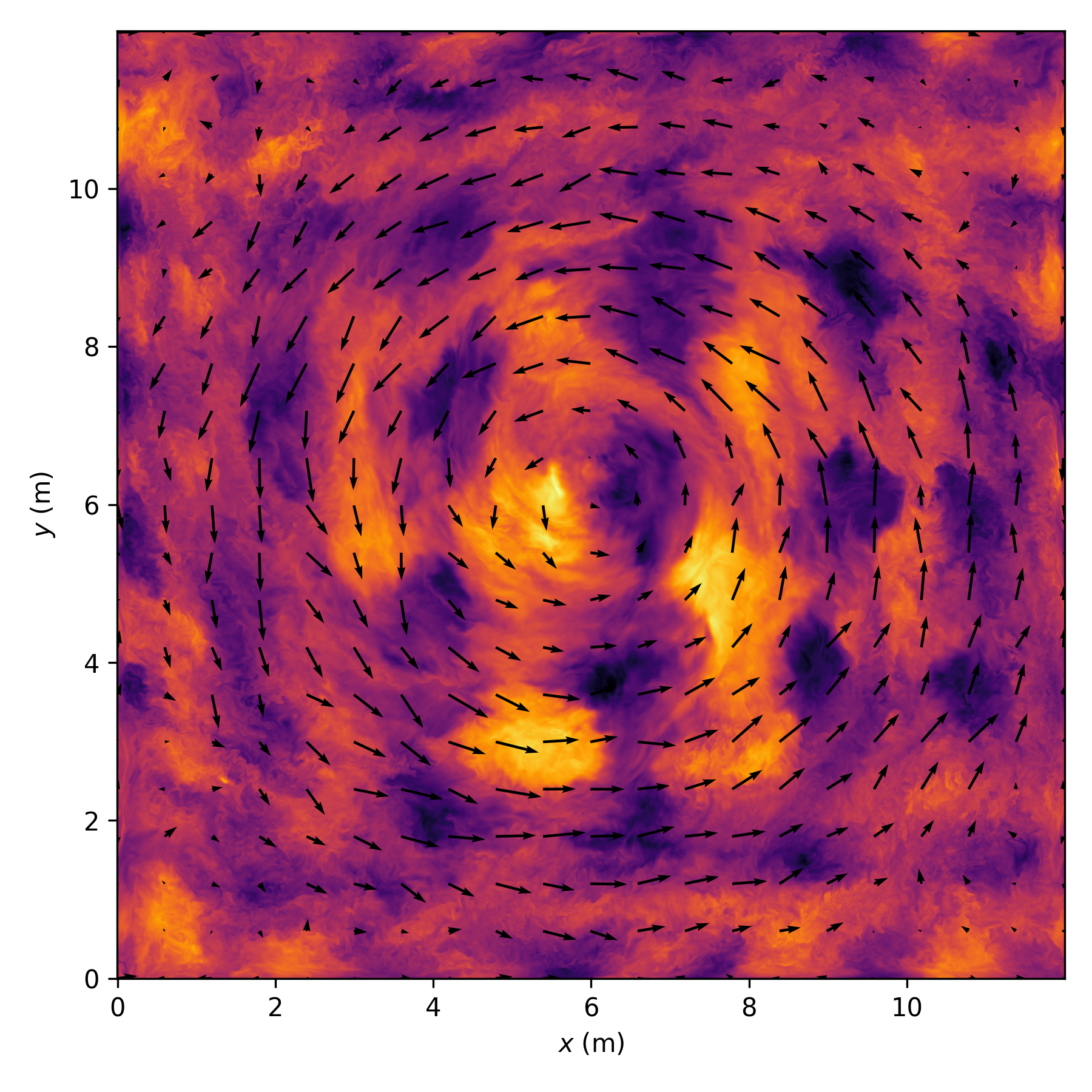
Figure 1. Horizontal cross-section of the buoyancy (colors) and velocity (vectors) for \(N = 0.6\) rad/s, forcing frequency \(0.73N\) and forcing amplitude 10 cm. The checkerboard pattern corresponds to the large waves forced at the periphery of the numerical domain.